精选的正方体的截面： 从原理上了解立体几何中截面

如何解决立体几何中截面图形问题

2018年全国一卷选择题压轴题

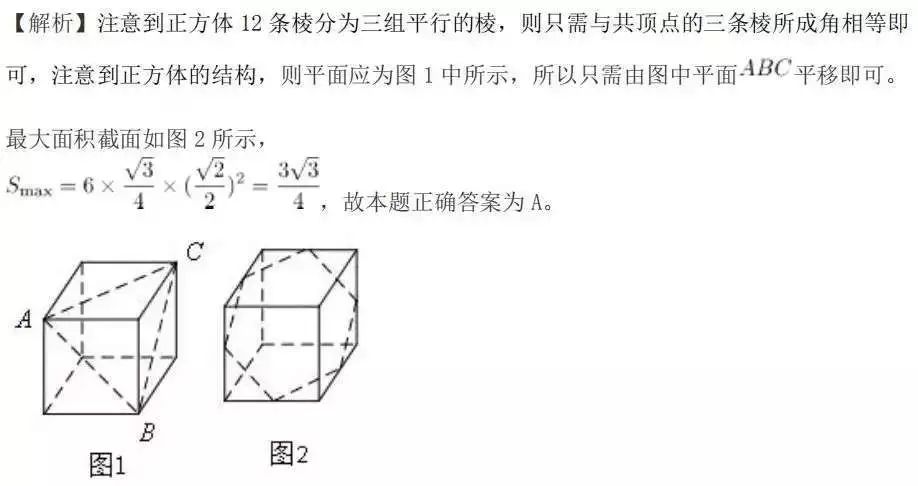
由此我们应该对截面问题进行一下总结

立体几何截面图定义

首先，多面体的截面在课本必修二P59─例3、P63─B─1处体现。我们要清楚截面的定义：在立体几何中，截面是指用一个平面去截一个几何体（包括圆柱，圆锥，球，棱柱，棱锥、长方体，正方体等等），得到的平面图形，叫截面。其次，我们要清楚立体图形的截面方式，总共有三种，分别为横截、竖截、斜截。最后，我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。

• 01

  正六面体的基本斜截面

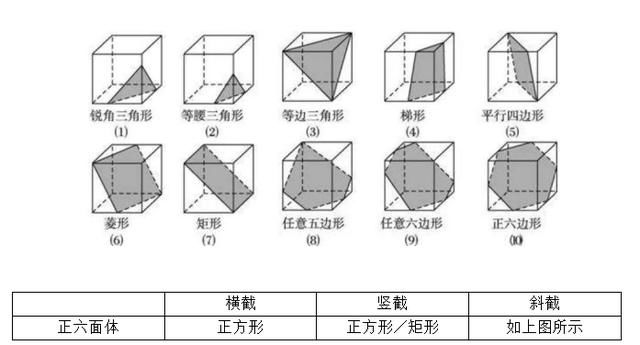
• 02

  圆柱体的基本截面

• 我们常考的立体图形截面多以六面体为主，在六面体的基础上再叠加一些圆柱、三棱锥等其他图形。我们在解题的过程中，只需要把每一个立体图形的截面记住，并在考试中熟练应用就可以解决很多题型了。

例1

一圆柱如图所示从中挖掉一个圆锥体，然后从任意面剖开，下面哪一项不可能是该圆柱的截面？

【解析】A是竖着切，B是横着切，D是从底面在不触碰中间小圆的情况下向外斜着切。C是斜着切，圆锥斜切的截面是个椭圆，但是位置应该偏向于一边，而不应该处于正中心。故答案为C。

例2

一立方体如图所示从中挖掉一个四棱锥，然后从任意面剖开，下面哪一项不可能是该立方体的截面？

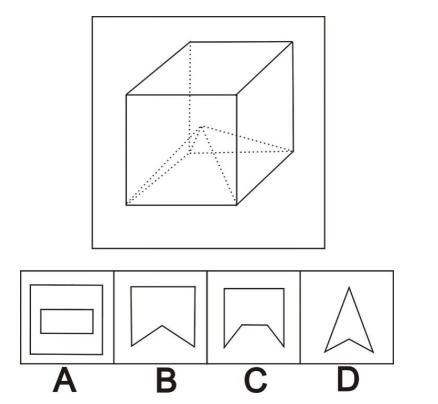
【解析】B是竖着切，C是从正方体一个侧面出发斜着向下切。D是从正方体一个侧边出发，斜着向下切。A选项四棱锥不能切出长方形，内侧出现长方形就是错误的。故选A。

例3

一圆锥如图所示，在上面叠加一个正方体，然后从任意面剖开，下面哪一项不可能是该立体图形的截面？

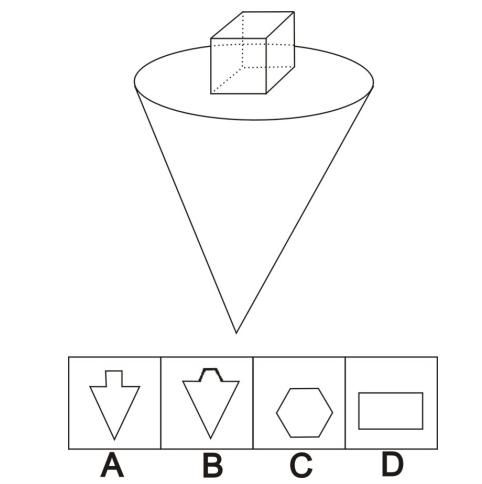
【解析】A是竖着切，B是从棱锥的顶点出发斜着向上切，D只要找到有四个面符合正方体的特征，一定可以切出。C必须有六个面符合正方体的特征，题干中正方体只有五个面，底面和圆锥重合，不符合正方体特征。故选C。

例4

一立方体如图所示从中挖掉一个圆锥体，然后从任意面剖开，下面哪一项不可能是该立方体的截面？

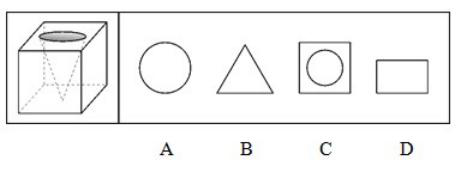
【解析】BD一定可以切出。C是立体图形的横切面，而A项是不可能得到的截面。故正确答案为A。

例5

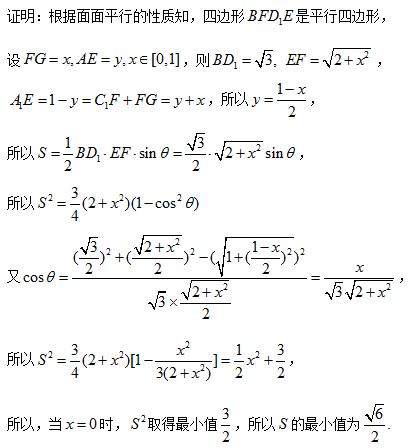
例6

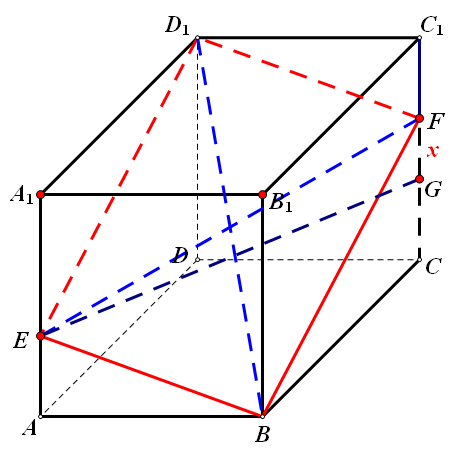
如图，正方体ABCD―A1B1C1D1中，E、F、G分别在AB、BC、DD1上，求作过E、F、G三点的截面．

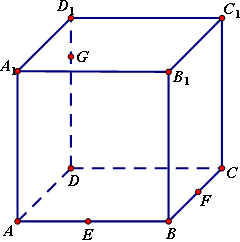
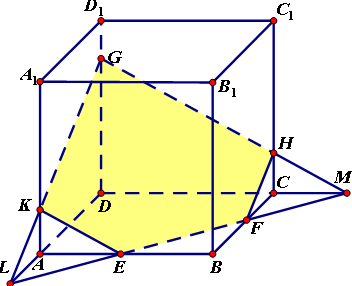
作法：(1)在底面AC内，过E、F作直线EF分别与DA、DC的延长线交于L、M．

(2)在侧面A1D内，连结LG交AA1于K．

(3)在侧面D1C内，连结GM交CC1于H．

(4)连结KE、FH．则五边形EFHFK即为所求的截面．

例7

P、Q、R三点分别在直四棱柱AC1的棱BB1、CC1和DD1上，试画出过P、Q、R三点的截面．

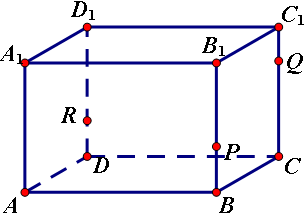
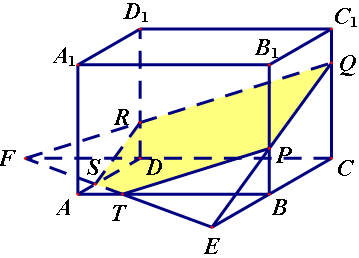
作法：(1)连接QP、QR并延长，分别交CB、CD的延长线于E、F.

(2)连接EF交AB于Ｔ，交AD于S．

(3)连接RS、TP。则多边形PQRST即为所求截面。

例8

已知P、Q、R分别是四棱柱ABCD―A1B1C1D1的棱CD、DD1和AA1上的点，且QR与AD不平行，求作过这三点的截面。

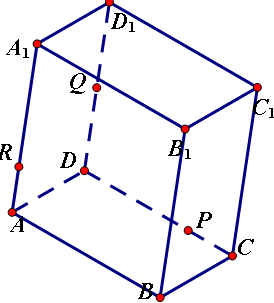
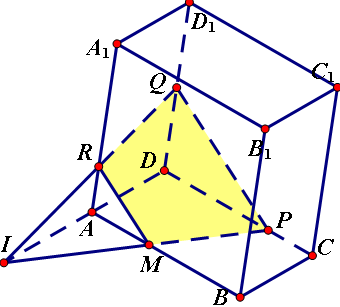
作法：(1)连接QP并延长交DA延长线于点I。

(2)在平面ABCD内连接PI交AB于点M。

(3)连接QP、RM。则四边形PQRM即为所求。

例9

在侧棱和高的夹角为α的正四棱锥中，求作一个过底面顶点且与这点所对侧棱垂直的截面(α＜45°)。

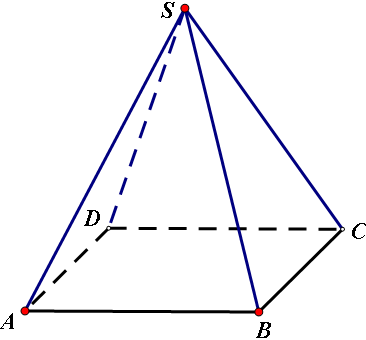
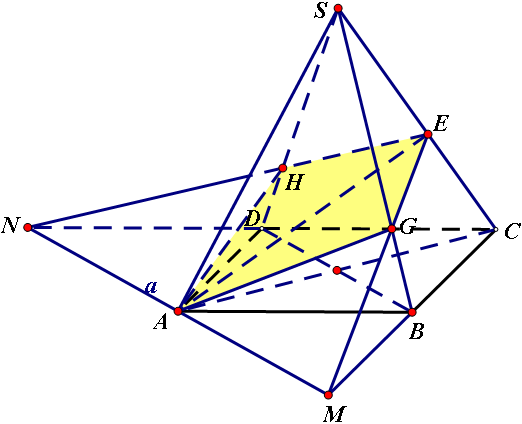
作法：(1)在平面SAC中，作AE⊥SC于点E。

(2)在底面ABCD内过A作a∥BD。

(3)延长CB、CD分别交a于点M、N。

(4)连接EM、EN，分别交SB、SD于点G、H。

(5)连接AG、AH。则多边形AGEH即为所求。

通过这些例题，我们不难发现，当你把每一个立体图形的截面知识都掌握好之后，我们再遇到多个立体图形的叠加，这些问题也都不在话下，相信同学们掌握以上知识点，都可以做好立体截面图形题。

最新正方体的截面： 从原理上了解立体几何中截面可以看看这篇名叫蚜虫防治：分布广、危害大，最新研究提示蚜虫防治新思路的文章，可能你会获得更多正方体的截面： 从原理上了解立体几何中截面

以下是的一些我们精选的蚜虫防治：分布广、危害大，最新研究提示蚜虫防治新思路

原标题：分布广、危害大，最新研究提示蚜虫防治新思路

新京报讯（记者 张一川）地球气候多种多样，影响到植物的生长分布，也影响到以植物为食的昆虫的分布。《美国科学院院刊（PNAS）》11月18日在线发表的论文中指出，蚜虫体内的共生菌对于蚜虫的耐热性有重要影响。“而耐热性则影响了蚜虫的分布范围。”论文第一作者、中国农业科学院植物保护研究所副研究员张博表示。

蚜虫在世界范围内分布十分广泛，尤其集中于中国大部分领土所处的北温带。“蚜虫在农业生产中危害也比较大，特别是在小麦、园艺上危害很大。”张博说。全国农业技术推广服务中心病虫害测报处处长刘万才等人的统计和研究显示，小麦蚜虫是2006年至2015年十年间影响全国粮食生产最为重要的“十大病虫害”之一。

在本次研究中，张博等研究人员选取了自然界分布最广泛的4种蚜虫，以及遗传信息被人类充分了解研究的豌豆蚜，共计5个品种6个品系的蚜虫进行研究。研究人员在实验中设置了致死温度38℃和亚致死温度37℃，不耐热品种在致死温度中存活率会显著下降，在亚致死温度中生育率和繁殖力都受到了影响。同时，研究人员还观测到不耐热蚜虫的共生细菌布赫纳氏菌数量下降，以及细菌细胞的变形和收缩。对基因数量和转录反应的分析表明，不同耐热性蚜虫体内共生菌小分子热激蛋白的表达差异，而这又源自蚜虫体内的共生菌是否具有对应的基因突变。

“由此说明共生菌是影响蚜虫分布的一个因子，也是控制种群动态的一个因子。”张博表示，基于研究，在传统农药针对昆虫各类细胞受体的思路之外，还可以考虑将共生菌作为新型农药的靶点。

新京报记者 张一川

编辑 穆祥桐 校对 危卓