精选的立体几何定理：高考立体几何点线面八大定理，每年都以解答题和选

线面位置关系的八大定理

一、直线与线面平行的判定定理

二、直线与线面平行的性质定理

三、平面与线面平面的判定定理

四、平面与平面平行的性质定理

五、直线与线面垂直的判定定理

六、直线与线面垂直的性质定理

七、平面与平面平垂直的判定定理

八、平面与平面平垂直的性质定理

考点分析：空间点线面的位置关系

典型例题1

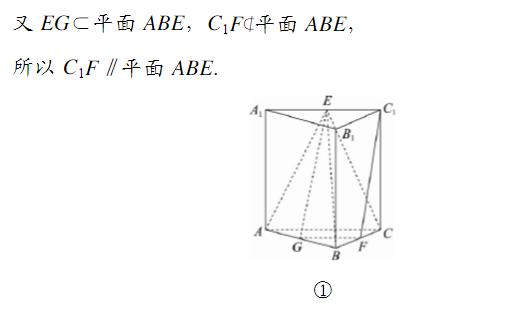
精华提炼

1.证明面面垂直，将“面面垂直”问题转化为“线面垂直”问题，再将“线面垂直”问题转化为“线线垂直”问题.

2.计算几何体的体积时，能直接用公式时，关键是确定几何体的高，若不能直接用公式时，注意进行体积的转化

典型例题2—全面了解正方体

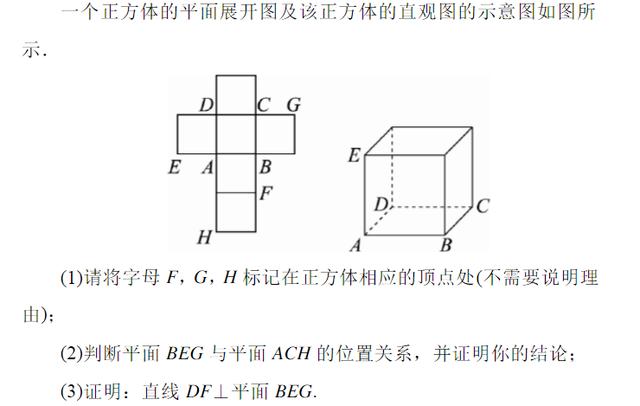
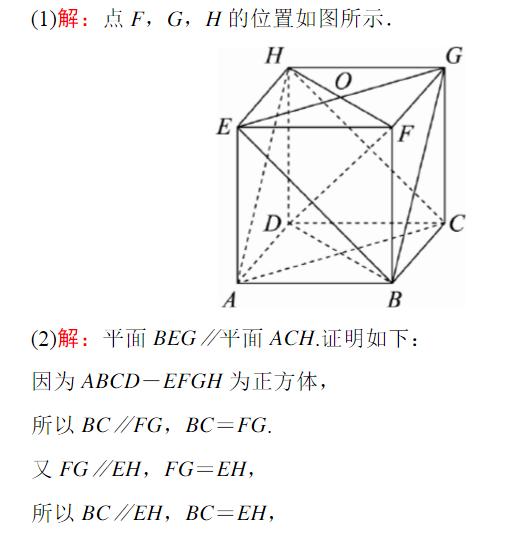
感谢大家的支持，高考即将来临，最近一段时间会着重分享高中知识，谢谢大家，有薄弱点的话，可以留言，我们也会安排老师针对薄弱点整理复习资料，祝：高考学子都考出理想的好成绩！

最新立体几何定理：高考立体几何点线面八大定理，每年都以解答题和选可以看看这篇名叫正弦定理公式：2020年高考加油，每日一题2：正弦定理有关的解答的文章，可能你会获得更多立体几何定理：高考立体几何点线面八大定理，每年都以解答题和选

精选的正弦定理公式：2020年高考加油，每日一题2：正弦定理有关的解答

典型例题分析1：

已知△ABC中，内角A，B，C所对的对边分别为a，b，c，且a+b=√3c，2sin2C=3sinAsinB．

（1）求∠C；

（2）若S△ABC=√3，求c．

解：（Ⅰ）∵△ABC中2sin2C=3sinAsinB，

∴sin2C=3/2·sinAsinB，故c2=3/2·ab，

又∵a+b=√3c，

∴a2+b2+2ab=3c2，

由余弦定理可得cosC=（a2+b2-c2）/2ab

=（2c2-2ab）/2ab

=ab/2ab=1/2，

∴C=π/3．

（Ⅱ）∵S△ABC=1/2·absinC=√3ab/4=√3，

∴ab=4，又c2=3/2·ab=3/2×4=6，

∴c=√6．

考点分析：

正弦定理；余弦定理．

题干分析：

（Ⅰ）由已知式子和正弦定理可得c2=3ab/2，结合a+b=√3和余弦定理可得cosC，可得角C；

（Ⅱ） 由三角形的面积公式可得ab=4，整体代入余弦定理计算可得．

典型例题分析2：

考点分析：

正弦定理．

题干分析：

（I）利用诱导公式、正弦定理，结合和角的正弦公式，化简，即可求角C的大小；

（Ⅱ）若c=4，△ABC的面积为4√3，求出a=b=4，即可求向量在方向上的投影．

典型例题分析3：

设锐角△ABC的三个内角A，B，C所对的边分别为a，b，c，且√3ccosA+√3acosC=2asinB

（1）求A

（2）若△ABC的面积为2√3，求实数a的最小值．

解：（1）∵√3ccosA+√3acosC=2asinB，

∴√3sinCcosA+√3sinAcosC=2sinAsinB，

∴√3sin（C+A）=√3sinB=2sinAsinB，

∵sinB≠0，

∴sinA=√3/2．

∵A为锐角，

∴A=π/3．

（2）1/2·bcsinπ/3=2√3，可得bc=8．

由余弦定理可得：a2=b2+c2-2bccosπ/3≥2bc﹣bc=bc=8，

当且仅当b=c=2√2时取等号．

∴a≥2√2．

∴a的最小值为2√2．

考点分析：

正弦定理；三角形中的几何计算．

题干分析：

（1）由√3ccosA+√3acosC=2asinB，利用正弦定理可得：

√3 sinCcosA+√3sinAcosC=2sinAsinB利用和差公式、诱导公式化简即可得出．

（2）1/2·bcsinπ/3=2√3，可得bc=8．由余弦定理可得：a2=b2+c2-2bccosπ/3，再利用基本不等式的性质即可得出．

最新正弦定理公式：2020年高考加油，每日一题2：正弦定理有关的解答可以看看这篇名叫真网友！华裔少年与澳神童网识6月合力发现新数学定理[鼓掌]的文章，可能你会获得更多正弦定理公式：2020年高考加油，每日一题2：正弦定理有关的解答

以下是的一些我们精选的真网友！ 华裔少年与澳神童网识6月 合力发现新数学定理[鼓掌]

原标题：真网友！ 华裔少年与澳神童网识6月 合力发现新数学定理[鼓掌]

近日，17岁的美国华裔少年梁徐明与一名17岁澳大利亚神童，网识6月后，合作发现新数学定理——可协助理解计算出立体几何结构，解题速度比计算机还快！数学家大赞将改变数学未来。#神童网友合创数学定理# 网友：史上最强网友！@@中国日报