精选的理发师悖论： “理发师悖论”引发第3次数学危机，至今

先跟大家分享一个有趣的小故事：有一位理发师开了一家理发店，突发奇想在店门口树立了一块牌子，上面写着：“我只给所有不给自己刮胡子的人刮胡子”，也就是说，凡是自己动手刮过胡子的人，都没有办法到这家理发店来刮胡子。

可是有一天，理发师发现自己的胡子变长了，当他拿起刮胡刀准备刮胡子的时候，突然想起来自己门口的那张告示，如果此时理发师自己刮了胡子，那么就违背了自己许下的诺言，可是如果他不刮胡子，也同样违背了自己的初衷。所以，无论从哪个角度看，这名理发师的“告示”都是一个悖论，这条悖论在数学界也被称为“理发师悖论”，用来解释“集合论”这个概念中所存在的严重逻辑问题。

其实在数学界，从这门学科创立至今，一直都存在着很多“危机”，简单来说就是在数学中，伴随着发展和探索的深入，各类矛盾也便涌现了出来，比方说有理数和无理数、加法与减法、实数与虚数等等，很多问题时至今日都没有一个明确的标准答案，并且伴随着时间的推移，各类难题根深蒂固，最终都变成了无法解决的数学“危机”。

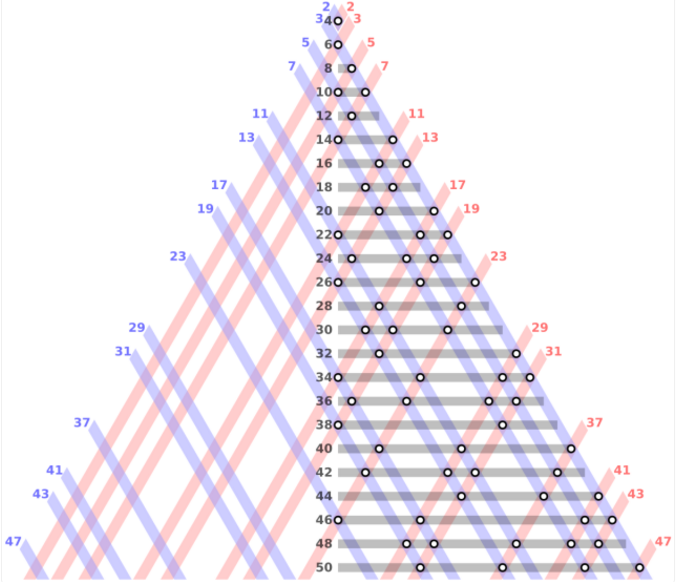
一旦“危机”得到合理的解决，那么对于整个数学界来说，都是一场革命！目前，数学界一共存在着3大危机，分别为集合、无理数、微积分等数学概念，第一个数学危机发生于公元前5世纪，是一场“无理数”危机，当时希波斯发现等腰直角三角形的斜边永远无法用最简整数比来表示，从此数学界中的“无理数”定义被首次发现。

第二个危机是微积分的合理性，当时在数学界引起了重大变革，差一点就将微积分从数学的概念中删除；第三个危机则跟“集合”有关，又被称为“罗素悖论”，这场数学危机爆发于1897年，一直到今天，数学界仍然找不到一个合理的解释，并且让整个数学概念的基本结构都发生了前所未有的质疑，也正是第三次数学危机，数学界中又诞生了一个新的学科——逻辑学。

其实早在罗素悖论提出之前，就有数学家对于“集合”存在着一定的疑虑，而罗素在他的基础上将“集合”中所存在的矛盾给放大，按照罗素的说法，假设“集合A={x | x A }，那么AA是否成立？1. 成立，那么x∈A，不满足A的特征性质。2. 不成立，A就满足了特征性质。”

当罗素提出这个概念之后，弗雷格苦心专研了12年的《算术的基本法则》毁之一炬，用弗雷格的话来说，好不容易等来了光明，却被罗素一把推进了黑暗之中。因为罗素悖论，整本《算术的基本法则》中的内容全都是错的，这对于一位数学家来说，是非常难堪的，也很难接受的事情。如今虽然在一定程度上，罗素悖论已经被破解，但是数学界还是存在着很多的质疑，未来当一切真正被揭开，那么“数学”将进入新的里程碑阶段。